雨戸 交換 自分 で質点系の運動方程式 | 高校物理の備忘録. 質点系の運動方程式. 全質量が M の多数の質点からなる系の個々の運動方程式を足し合わせると, 系の重心 r G と外力 F ext との間に次式が成立する. M d 2 r G d t 2 = F ext. 系の全運動量 P は系の重心の運動量 P G = M v G と一致する. P = P G. 系の全運動量 (=系 . PDF 9章 質点系の力学(1) - 東京工業大学. 質点系にはたらく力は,質点系の外から作用する外力2. 
と,系を構成する2つの質点の間に作用する内力に分けられる。 2つの質点の運動方程式は. d2r1. = + , dt2 F F 1 21 1. d2r2 m1 = +. F F 2 dt2 12 2. (9.1) O. 12 m2. F21 F. 
と表せる(図9.1下)。 ここに,と. 犬 目の下 腫れ
ギター 指 を 鍛えるF 1. はそれぞれ. F 2. 質点1と質点2に作用する外力である。 とは. F F 21 12. 内力で,前者は質点1が質点2から受ける力,後者はF1. 質点2が質点1から受ける力を表す。 ニュートンの運動F2. の第3法則(作用・反作用の法則)により図9.1:2つの質点からなる系.上: F = 21 F 12. PDF 質点の力学と微分方程式 - 広島大学. 質点の運動の記述. v(t) = dr(t) dt. 速度. r(t) : 時刻 における t 質点の位置ベクトル. 質点の運動の記述. 歯医者 c2 とは
パソコン から 読み取り を 開始 できる 状態 にし て くださいa(t) = dv(t) dt. = d2 r(t) dt2. 加速度. chpl とは
土鍋 ih ご飯 炊き 方r(t) O. ベクトル値関数の微分. r(t), v(t), a(t) は実数 にベクトルを対応させる関数t. ベクトル値関数. 例えば. r(t) = (x(t), y(t), z(t)) に対し. dr(t) = dt. dx(t) dy(t) dz(t) , , = ( dt dt dt. ̇x(t), ̇y(t), ̇z(t)) d2 r(t) = dt2. d2x(t) d2y(t) d2z(t) dt2 ,. PDF 2章 1次元の運動(1) - 東京工業大学. 2.1 運動方程式の解と初期条件 質量m の質点がx 軸上を力F(x,t) を受けて運動する場合を考える。質点の位置をx(t) で表して,運動方程式は m d2x(t) dt2 = F(x,t) (2.1) と書ける。「運動方程式が書ける」とは,質点が時刻t に位置x(t) F(). PDF 質点と剛体の静力学と動力学 - 東京工業大学. 運動方程式を用いれば,個々の物体に働く力や力のモーメントか ら物体の運動を知ることができる.物体の運動を扱う力学を動力学 や運動力学等とよぶ.逆に物体が静止している時の状態を扱う力学 を静力学とよぶ. 1.5 トラス構造とラーメン. PDF 10章 質点系の力学(2) - 東京工業大学. 運動方程式. ぞれぞれの質点の運動方程式は. d2rj. N. = +. dt2 F ij F j. 雀 の ふん 病気
郵便 局 で ダンボール 買える(j = 1, 2, , N) · ·. (10.1) i=1. と書ける(2質点系の場合の(9.1) に対応)。 ここに,右辺の最後の項は質点jにはたらく外力である。 右辺の第1項は質点系を構成する他の質点から質点jにはたらく内力で,和の記号に付けたはi = jを除くことを意味する。 作用・反作用の法則から=が. F ij − F ji. 成り立つ。 質量中心. 質点系の質量中心(重心)の位置ベクトルは. rG. m. j rj. m. j rj. = j=1. = j=1. rG. N M. (10.2) m. j=1. で与えられる((9.4)に対応)。. PDF 質点系の運動 - 東京都立大学 公式サイト. つの質点の3 次元運動:3 自由度(変数x, y, z) 2 質点系は6 自由度(変数x1, y1, z1, x2, y2, z2) 外力と内力. 質点1 にはたらく力:外力F1 と質点2 からの内力F1 2. 質点2 にはたらく力:外力F2 と質点1 からの内力F2 1. 例)太陽の重力中の地球(質点1 )と月(質点2) F1 :太陽が地球に . PDF 質点系の運動. 各成分を数えると式. 2. 1. (24) に3 本、式(25) に. (25) 3 本、合計. 6本(自由度の数)の運動方程式. 
• 作用反作用の法則(運動の第3法則) = 2 F1 F2 1. F1 2 + F2. 1 = 0. (26) 意味:内力の和はゼロ. 5. 2.2 重心座標の運動方程式. 重心. (質量中心)座標:. 剛体の運動方程式 - 物理メモ. 2018.03.01. 剛体の運動方程式. Tweet. [mathjax] 力を加えても変形しない物体を 剛体 という。 そして、剛体は質点の集合体とみなすことができる。 この記事では、剛体の運動方程式を導出してみる。 M d 2 r G d t 2 = ∑ i = 1 N F i. 目次 [ hide] 1 j番目の質点の運動方程式. 1.1 質点同士の相互作用と内力. 1.2 外力と運動方程式. 2 質点系全体の運動方程式. 2.1 内力の総和. 2.2 質点系全体の運動方程式. 3 重心を使った運動方程式. 4 剛体の回転運動について. 5 まとめ. 6 参考文献. j番目の質点の運動方程式. 質点同士の相互作用と内力. 上図のように、2つの質点の間には力が働いている。. ニュートンの運動法則と質点系の力学|質点系の力学から連続 . L = m r × v = r × p. 各質点の角運動量を合計すると、質点系の角運動量が求まります。. L = ∑ i = 1 N L i = ∑ i = 1 N ( m i r i × v i) = ∑ i = 1 N ( r i × p i) 両辺を微分して、. d L d t = d d t ∑ i = 1 N ( r i × p i) = ∑ i = 1 N ( r i × d p i d t) = ∑ i = 1 N ( r i × F i ′) = ∑ . 質点の力学 - t-kougei.ac.jp. 質点の力学. 4.運動方程式による運動の解析. これまで見てきたように、物体に作用する力と運動の初期条件がわかると、物体の運動は一意的に決定される。 これは、 (1) (物体に作用する力)の式に基づいて、運動方程式をたてる。 (2)上記の微分方程式を、与えられた運動の初期条件(時刻0における物体の位置と初速)のもとで解く。 の手順で求められる。 例えば、滑らかな床の上で、質量 m の物体を 初速度v 0 で水平に投げ出したときの運動について考える。 ただしこの場合、物体は速度 v の自乗に比例する -kv 2 の抵抗力 を受けるものとする。 時刻tにおける物体の速度をv (t)とすると、運動方程式は. で、 この場合の運動の初期条件はv (0)= v 0 である 。 これは、. PDF 一様な重力場中の質点の運動 - 福岡大学. 一様な重力場中の質点の運動. 前章で運動方程式が提示されたので,本章を含むいくつかの章で具体的な力が与えられたときに運動方程式を解いて, その力の作用のもとでの物体の運動を考察してみよう. 5.1 目的,理想化. 地球上で起こる日常経験する物体の運動を考察する.物体をもちろん質点と理想化して扱う. その他にも問題を簡単化するために, 以下で述べるいくつかの理想化を行う.地球上の物体には, 地球による引力が働いている. この引力は重力と呼ばれている.重力の大きさは物体の質量に比例し, その方向は地球の中心を向く方向である.単位質量当たりの物体に働く重力をg と表す. 1 kg の物体に働く重力の大きさg jgは地球の緯. j. 度, 経度, 高度に依存して変化することが知られている. 一般の質点の運動. 一般の質点の運動. これまでは,簡単に解がわかる特別な場合の質点の運動をみてきた。 より一般的な場合でも,力が与えられれば,以下のように運動を決めることができる。 力 が具体的に与えられていると, 運動方程式 が書ける。 運動方程式は2階の常微分方程式であるが,その 一般解 が具体的に(陽に)書ける場合もあるし,書けない場合もある。 一般解が書ける場合には, 初期条件 を与えると 特解 が決まり,具体的な運動(各時刻の質点の位置)が決まる。 一般解が書けない場合でも, 初期条件 を与えると,その後の運動を 数値計算 で求めることができる。 質点の運動方程式の解を求める作業には,数学で言う「常微分方程式の解法」が必要になる。. PDF 6. 質点の力学. 質点の力学. ニュートンの運動の第2法則. 質点に加わっている力は, 質点の 質量と加速度の積に等しい. 微分方程式で書くと. または. Isaac NEWTON (1642 - 1727) ニュートンの運動の第2法則. ma = f. dv. = f. dt. d2 r. = f. dt2. バネ振り子の運動は. x(t) 1次元運動. x. 自然長からの伸び. x(t) で記述. 弾性限界内では、弾性体に加えられた力と歪み (伸び・ちぢみ)の量は比例する. フックの法則(Hookes Law) 単振動の方程式. コーヒー で 染める
茶屋 の 餅 青森バネの復元力. Ex. 6-1. x(t) の満たすべき微分方程式を求めよ. m : おもりの質量. k : バネ定数摩擦は無視できる. d2 x. 様々な運動 / 大学物理入門(A guide for University Physics). ニュートンの運動方程式. 質点の運動を記述する方程式。 力学の基本として、非常に有名な式です。 式はma=Fと書きますが、これは「力とは質量と加速度を掛け合わせたものである」という意味ではないことに注意してください。 詳しくは「新・物理入門」(駿台文庫)を参照。 動摩擦力を伴う直進運動. なめらかではない床の上での剛体の運動 を求めましょう。 剛体の質量をm [kg]とし、時間0 [s]における質点の位置を0 [m],速度をv 0 [m/s]とします。 さらに計算を簡単にする為に、質点はX軸上を運動するものとします。 物体の初速と摩擦力を示したのが次の図です。 力と速度を混同して表記しており、自由物体図ではないことに注意してください。. PDF 振動工学の基礎(1質点1要素系の運動方程式) - Tcu. 質量m,剛性kを有する系の運動方程式(非減衰自由振動)は次のように表される.. mx&&+kx=0(2.1) 式(2.1)の両辺をmで除し, =ω. m k(2.2) とおくと,次式が得られる.. x&&+ω2x=0 (2.3) この一般解は微分方程式論よりC1,C2を任意定数として次のように求まる.. x=C1cosωt+C2sinωt(2.4) x&=−C1ωsinωt+C2ωcosωt(2.5) 任意定数C1,C2は次の初期条件より求まる.. t=0→ , x=x0x&=x& 0. - -1 . 武蔵工業大学 コンクリート研究室. C1=x0, ω. 0 2. x& C=(2.6) したがって,式(2.3)の特殊解は次のように表される. 質点系の運動の分離 | 高校物理の備忘録. 質点系の運動方程式 では, 系の全質量が重心に集中した仮想的な質点の運動量と系の全運動量とが一致することを示し, 系に働く全外力 F ext が重心に集中したとみなした運動方程式 M d 2 r G d t 2 = F ext で重心の時間発展が理解できることを学んだ. ほかにも数多の議論を通して, 重心 が質点系を特徴づける特別な点であることは明白であろう. 実際, 2体問題 の項では2物体の運動エネルギーは 重心運動エネルギー と 相対運動エネルギー とに分離可能なことを示した. そこで, 系の持つ重要な物理量 ( 運動量 や 運動エネルギー, 角運動量 など)が 重心の運動 と 重心に対する相対的な運動 とに分離可能であることを示す. PDF 第8回:2質点系モデルの振動解析、および、様々な建物と地震動. 図1.1 に建物の2質点系振動モデルと地動加速度により各質点に作用する力(慣性力・減衰力・復元力)とつり合い式(運動方程式)を示す。 2層 建物変位. 質量. x 2( t ) 減衰係数 剛性. 2 x − x. 1. 建物変位. x 2( t ) −. m. 慣性力減衰力復元力. 力のつり合い式 { x ( t ) + y ( t ) } − c { x 2 ( t ) − x ( t ) } − k { x ( t ) − x 2 2 2 1 2 1 ( t ) 2 } = 0. 1層. 質量. (運動方程式) x 1( t ) −. 慣性力減衰力 復元力. PDF 質点系と剛体の運動方程式. 個の質点がなんの束縛も受けずに自由に運動している場合,その運動は 3 つの独立変数で表 すことができます。 この変数は通常 3 次元直交座標 (x; y; z) か球面座標 (r; μ; Á) が採用されます が,独立変数の数を 自由度 といいます。. 質点ってなに?わかりやすく解説 | 受験物理ラボ. 高校物理の範囲で扱う 等速直線運動 や 放物運動 は、基本的に質点の運動として考えます。 なぜ質点が発明された? 質点が便利なのは「 大きさを無視することができる 」という点にあります。 例えば以下の画像のように、重さのある球体を坂に置いたとしましょう。 このとき球体はどんな運動をするでしょうか? そう、転がりながら坂を降りますよね。 大きさのある物体は回転する. 大きさを考慮しなければいけないとき、物体には必ず回転の作用が働きます。 ですが回転の作用を式で計算しようとすると、考えるべき項目が増えてしまいますよね。 ましてや高校物理の範囲内でで物体の回転まで考えて問題を解こうとすると、難易度が上がってしまいます。 そこで使われるのが質点です。. PDF 11章 剛体の運動(1) - 東京工業大学. 質量中心の運動は質点の運動と全く同様に扱うことができる。 剛体の質量中心は,質点系の質量中心と同様に,剛体がN個の質点からなると考えれば. N N = . , M = m. PDF 質点系の運動 - 東京都立大学 公式サイト. F. 2. アップル ペンシル 折れ た
中 3 理科 エネルギー の 移り変わり1 2 F. m1 m2. 感光 体 と は
公園 の ブランコr1. r2. O. 図14: 2質点系にはたらく力の例。 外力か内力かは系の範囲によって決まる例)太陽も系に含める場合は、太陽が地球におよぼす重力F1は内力. 運動方程式. :地球が月におよぼす重力. d2r1. m1 = F1 + F1 dt2 d2r2 m2 = F2 + F2 dt2. 各成分を数えると式. 2. 1. (108) (109) に. 3 本、式(109) に. 3 本、合計. 6本(自由度の数)の運動方程式. 25. 作用反作用の法則(運動の第. 
3. 法則) = 2 F1 F2. 1. F1. 2024年 慶應理工 力学 解説|わかゆう - note(ノート). 投射問題はv-tグラフor運動方程式から時間追跡すればよい。 衝突問題は運動量保存則と反発の式を連立すればよい。図 図c-1 図c-2 図c-3 解説 (3)池ポチャ単振動 単振動の問題は式を頼りに考えるとよい。実際は物体が水面で単振動して . syllabus.adm.nagoya-u.ac.jp. 現代科学技術における重要な基礎分野の一つである古典力学の基礎を,慣性系における1個の質点の運動を例にとって講義します。力,質量,運動量,仕事,エネルギー,保存則,運動方程式,次元解析などの物理的概念に加え,座標系,ベクトル,ベクトル演算などの数学的概念を説明します。. PDF 数理物理学としての 微分方程式序論. 束縛された質点の等速運動を微分方程式によって特徴付け,その周期運動の軌 跡の媒介変数表示を通じて三角関数が自然に現れてくる様子を記述する. 8.1 調和写像の模型化としてのニュートンの運動方程式の 導入 H を内積(·|·) を . #74_当事者の醍醐味・当事者の苦悩|せっちー - note(ノート). バスケ部の子と話をした。 わたしは副顧問。 顧問の練習スタイルが合わないらしい。 バスケットボールはど素人で、ルールもある程度しかわからない。 練習メニューも全然。 顧問は10年バスケをしていた初任の子。 ルールはもちろん、練習メニューも試合中のアドバイスも的確で、ずっと . 花菜 っ 娘
出産 のし剛体の力学 - t-kougei.ac.jp. 2.1 慣性モーメント. 質量Mの質点に作用する力をF、その時刻での質点の速度をvとすると、質点の運動方程式は、 である。一方、慣性モーメントiの剛体に作用する力のモーメントをN、その時刻での角速度をωとすると、 である。これら、並進運動と回転運動に対する運動方程式を比較すると、. 慣性モーメントとは?回転の運動方程式をわかりやすく解説 | 機械設計エンジニア1年目の教科書. 回転の運動方程式を考えるときに必要なのが、「剛体」の概念です。 剛体とは、力を加えても変形しない仮想的な物体のこと。 質点と違って大きさや形を持った物体として扱えるので、「重心」や「慣性モーメント」といった物理量を考えることができます。. 質点:物理学解体新書. 
質点. home> 質点の力学>質点とは. 質点とは. 物体の並進運動を考える場合、物体の大きさや材質、回転や変形を考慮する必要はない。 大きさを考慮しない代わりに、「その物体の全質量が、その物体を代表する一点に集中している」と見なして論を進める。. ばねでつながれた調和振動子の二体問題|質量中心座標と換算質量 | 生命系のための理工学基礎. 二分子原子は、バネでつながれた二つの質点がなす系として近似できます。今回はこのモデル、いわゆる二体問題について運動方程式を立てることから始めて質量中心座標(重心座標)を導入し、相対座標と換算質量を用いた方程式の単純化についても触れていきます。. 剛体の運動方程式の導出(重心と慣性モーメント) - 物理学の見つけ方. よって、運動方程式()の第1式より、重心 の運動方程式は となり、第1章の質点のキャッチボールの場合と同じになる。また、回転部分については、同第2式よりトルクが発生しないので、重力は回転には影響しないことも分かる。. PDF 質点の運動 ver.20230419. Figure 1: 質点の変位と速度 一般に,質点の位置を,直交座標系における位置ベ クトル ⃗r = x ⃗i+yj +zk = (x,y,z) (1) で表すことにしよう.このベクトルは始点を原点に固 定するベクトルであることに注意.質点が運動してい る場合は,位置ベクトルが時間tの . PDF 質点の力学(1) - 工学院大学. Laws of Motion. Law-1: Every body continues in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed upon it. Law-2: The change of motion is proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed. 質点とは?1分でわかる意味、質点系、運動方程式との関係. 質点とは、大きさのない質量のかたまりです。. 建築物の振動解析(揺れ方)を行う時に使います。. 建築物は複雑なので、全てをモデル化するのは難しいです。. そこで質点に置き換えるのです。. 今回は、質点の意味、質点系、質点と運動方程式について . 【大学物理】剛体の力学入門②(重心の運動)/全6回【力学】 - YouTube. 最後まで見ろよ〜動画の内容に関する質問はコメント欄へどうぞ。また、今までの質問についての回答をまとめたq&aは固定コメントにあります-----. 斜面上での物体の運動を解説 (例題も2問あり)【物理基礎】 - YouTube. 【斜面上での物体の運動】重力の分解や運動方程式の作り方について解説。(1)滑らかな斜面上で質量mの物体を加速度aで引っ張るには何Nの力を . 【振動】垂直にバネで繋がった2質点の連成振動:運動方程式の立て方・解き方 | ばたぱら. 1. 運動方程式 以下のような垂直に2質点がバネで繋がっている時の連成振動を考えよう。質量 の質点について、つり合いの位置からの変位をそれぞれ として連成振動を見ていく。 初期状態を釣り合いの位置にすれば、重力は関係なくなる。. 円運動の公式まとめ(運動方程式・加速度・遠心力・向心力) | 理系ラボ. 東大塾長の山田です。 このページでは、円運動について「位置→速度→加速度」の順で詳しく説明したうえで、運動方程式をいかに立てるか、遠心力はどのように使えば良いか、などについて詳しくまとめてあります。 ぜひ勉強の参考にしてください! 1. 円 の 断面 二 次 モーメント
出産 祝い のし 連名動かして学ぶバイオメカニクス#7 〜オイラーの運動方程式と慣性モーメント〜|Sports Sensingスポーツ科学研究室. 本章から逆動力学計算を利用して関節のトルクの計算について述べていく.ニュートンの運動方程式と同様で,回転の運動方程式も再帰的に解くため,必要に応じてこのシリーズの復習も行っていただければと思う.なお,今回は実際にコードを動かして確認する作業は含まれない.次の . 運動方程式〜ニュートンの第2法則〜 | 高校生から味わう理論物理入門. 力学に登場する 「運動方程式」 (英:Equation of Motion, EOMと略されることもある)について,意味,利用例等を詳しく解説します。. ちなみに,慣性系とは,第1法則「慣性の法則」によって定義されます。慣性系については慣性の法則〜ニュートンの第1法則〜で紹介します。. PDF 2 ニュートンの運動方程式 - 北海道大学. 天体や地球上の自然現象が、(i)数式に従って秩序をもって運動し、(ii)予言 可能であることが明らかになったのである。その中心をなすのが、次のニュートンの運動方程式である。 2A5 m F 3ÿ Øa ニュートンの運動方程式 質量mの物体に力F⃗ が働くとき、この . PDF 解析力学B - 第06回: 質点の運動 - Kobe University. 自由度が2次元とは:質点の位置が二つの座標(x1,x2)で 指定される。 2次元の運動:時間の関数としての質点の位 置(x1(t),x2(t)) 重要ポイント:(x1,x2)はカーテシアン座標の(x,y)とは限ら ない。 ⇒二つのペアで位置が指定できるものあれば、どんな座標 でもいい。. 【古典力学】1体問題、2体問題、N体問題の運動方程式 | ばたぱら. この式は1体問題の運動方程式が単に2つあるだけで、それぞれの質点について運動方程式を解いてやればよい。. このように相互作用がない場合は、質点が独立に運動していることがわかる。. つぎに、2質点の間に相互作用がある場合を考える。. たとえば . PDF 2 質点系 - 兵庫県立大学理学部. 太陽・地球・月の質点系では、おたがいの間にはたらく万有引力は内力にあたるが、 太陽・地球のみの2体問題を考える際には、太陽と月間の万有引力は外力になる。 2.3.1 運動量保存の法則 質量ml、m2、…の質点の位置ベクトルをr1、r2、…、速度をv1、v2 . 
単振り子:運動方程式 - Kit 金沢工業大学. 単振り子 : 運動方程式 (equation of motion) 鉛直面内で 回転運動 できるように点 O で固定した軽い棒の先端に質量 m m の質点を取り付けた単振り子について,点 O から引いた鉛直軸 OC と棒とのなす角を θ θ とする(反時計回りに回転する角の向きを正にとる . ばねの運動方程式と減衰振動|微分方程式入門③【力学】【機械工学】 - 高校物理からはじめる工学部の物理学. ばねの運動を題材に、減衰振動の微分方程式の解法を解説します。 減衰振動に考える前に、まずは、減衰や強制振動の無いばねの運動を考えます。 このような運動を 単振動 と呼びます。. このとき、ばねの運動方程式(=微分方程式)は、以下のように表せます。. PDF 回転系上の運動方程式 - 福岡大学. 7.2 回転系における運動方程式 69 いっぽう, 遠心力の特徴は, • 回転軸から物体を結ぶ直線上で外向きに働く. • 回転軸からの距離に依存する大きさを持つ. 7.2 回転系における運動方程式 7.1 節で述べたように, 慣性系に対して一定の角速度Ω で回転している座標系で質点 . PDF 重心の運動 - 東京都立大学 公式サイト. 相対座標! r の運動は質量µの質点に内力F! 内がかかった運動と同じ このとき重心座標の運動方程式と全運動量P! は M d2R! dt2 =!0, dP! dt =!0 (154) • 外力のない2体問題は、換算質量と相対座標による1体問題と等価 (重心と相対に分解する意義) • 外力のないn体 . 中心力場の運動方程式 - Coocan. 中心力場の運動方程式. [←] [↑] [→] 【中心力場(球対称なポテンシャルU (r))の中の質点(位置r(t))に対する運動方程式】. 【エネルギーの保存】. 【角運動量の保存】. 運動はLに垂直な平面内にとどまる。. 目標は、逆2乗則の力の場合の運動方程式を直交座標で . 内力と外力とは?|定義と見分け方【力学基礎】 - 高校物理からはじめる工学部の物理学. 複数の質点や物体をまとめて一つのグループとして扱うとき、そのグループ内の物体が互いに作用しあう力を内力と呼び、外部からそのグループ内の物体に作用する力を外力と呼びます。. 例えば、複数の物体に重力がはたらいている場合、重力を及ぼす地球がそのグループに属していなけえれ . 力積と運動量の関係 | 高校生から味わう理論物理入門. 作用反作用の法則〜ニュートンの第3法則〜の記事の最後で,質点系の重心に関する運動方程式を導出しました。 この運動方程式に対して,前節と全く同じ流れで処理すると, p ‾ = c o n s t . overline{boldsymbol{p}} = mathrm{const.} p = const. を導けます。. 物体の落下運動と空気抵抗 - Kit 金沢工業大学. 解説. 次に, 空気抵抗 として,物体の 速度 v 〔m/s 〕 v 〔 m/s 〕 に比例した粘性抵抗力が落下の向きとは逆向きに働いている場合を考える.ただし 重力加速度 として g 〔m/s2 〕 g 〔 m/s 2 〕 を用いる.. (3) ( 3) 羽に対する運動方程式を示せ.ただし,羽に . 回転座標系 お 質点 運動方程式 - J-stage. 回転座標系における質点の運動方程式 空間に固定されたベ ク トル であるが,i ,j は回転に伴 い 時間変化する。i ,!をそれぞれ位置ベ クトル とする ような質点を考えると,これらの 質点は点0の 回りで半 径1の等速円運動を行なう。したが っ . 単振り子の微小振動|周期の公式を運動方程式から導出 | 高校生から味わう理論物理入門. 以上のことを踏まえると,単振り子において振動子は,円軌道を運動するとわかるので,向心方向と接線方向の運動方程式を立てればいいことがわかります。 . 振動子が質点ではなく,有限の大きさがある場合は,大学で扱うことになります。 . Sympyを使った運動方程式の導出と線形化 #Python - Qiita. はじめに. SympyはPythonの記号計算パッケージとして有名ですが、ラグランジュ法(ラグランジュの運動方程式)を用いて質点系の運動モデルを導出できる機能についてはあまり知られていないようです。. 少し調べてみたところなかなか便利そうなので、この . PDF .質点の運動. 1-3. 直線運動する質点の加速度(acceleration) 質点の運動の状態を調べるために,加速度(acceleration) a も重要な物理量となる.加速度は加速する度合いを表す量であり, 加速度aは,「単位時間(例えば,1 秒や1時間など・・)当たりの速度の変化」とする.. 物理に現れる『質点』とはそもそも何かをわかりやすく解説 | 黒猫の高校物理. 「物体の運動」は「質点の運動」とみなしてしまおう! では「質点」という考え方が 作り出された理由を述べていきます。 物体の位置を決めたい時. まず次のような状況を考えましょう。 今、床の上で引っ張られる 物体の運動を考えるとします。. 単振動の加速度にマイナスがつくのはなぜ?運動方程式の弾性力にマイナスがつく理由を丁寧に解説! | 黒猫の高校物理. ばねの単振動の運動方程式にはなぜ「マイナス」がつくの?フックの法則にマイナスがつくの?この謎を丁寧に解説! 黒猫の高校物理 力学 ばねの単振動の運動方程式 今回は次の図のような ばねによる単振動 において、運動方程式が $$Large m. ラグランジュの運動方程式の導出 - tknotebook. 仮想変位とはもともと静力学の概念で、時間の経過を伴わない、質点の実際の運動とは関係のない任意の変位です。つまり、静力学では、力が釣り合っているかどうかを判断するため、ちょっと仮に動かしてみて、エネルギーが吸収されたり放出されたりし . 単振り子:運動方程式 [ 直交座標系における導出 ]. 単振り子 : 運動方程式 (equation of motion) [ 直交座標系における導出 ] 鉛直面内で回転運動できるように点 O で固定した棒の先端に質量 m の質点を取り付けた単振り子について,図のように点 O を原点として,鉛直面内の鉛直下向きに x 軸,水平方向に y 軸を . 【解析力学】3質点の連成振動~オイラー・ラグランジュ方程式の利用例~②. 下記の続き。. 【解析力学】3質点の連成振動~オイラー・ラグランジュ方程式の利用例~①. 前回 にてオイラー・ラグランジュ方程式を導入したが、今回はその応用例を見ていく。. 以前扱った2質点の連成振動を3質点に拡張してみよう。. 問題 下図のように . 慣性モーメントと剛体の運動方程式|定義と計算例・平行軸の定理 【剛体力学】 - 高校物理からはじめる工学部の物理学. 慣性モーメントの定義. 慣性モーメントとは、『物体の回転させにくさ』を表した物理量です。. 剛体のように質量が空間に連続的に分布している物体 を考えるとき、並進運動に加えて回転運動も考えなければなりません。 回転運動を考える際、慣性モーメントは必要になります。. PDF 物理学基礎 I(医・医)第 12 回 多質点系の並進運動 重心運動と相対運動. 多質点系の力学 2 質点系の運動方程式:重心運動と相対運動 3.2. 2質点系の運動方程式:重心運動と相対運動(5) 一般的に,外力が働いていない系においては,系の全運動量が保存する. 運動量はエネルギーと並んで重要な保存量である.. 【物理】斜面を転がる球の運動(計算式・例題) | 西住工房. この記事では、物理学の斜面を転がる球の運動の計算式や例題について解説します。. 下図のように斜面を転がっていく球の運動について考えます。. 球を傾斜角θの斜面上に置いて静かに放したあと、地面に到達するまでの時間Tを求めよ。. となります . PDF 調和振動子(その1) バネに繋が れたおもりの振動. 摩擦のない水平な*1テーブルの上にある質量m の質点の運動を考察する. 水平方向に デカルト座標系のx 軸をとる. 質点の運動はx 方向のみの1 次元問題とする. 質点には バネ定数k の線形バネがつながれていて, 質点にはバネの復元力のみが働いているとす. PDF ニュートンの運動方程式と慣性力 - Kit 金沢工業大学. 運動の第3法則:作用と反作用は大きさが等しく向きは逆である. が成立し,これら3 つの法則が(Newton の)運動の法則といわれている.そうして,この運動の 法則が成り立つ空間が在ったとしてこれを慣性系というわけである.今後,物体が運動している. 質点と剛体 - 高校物理をあきらめる前に. 大きさをもち,力を加えても変形しない物体のことを剛体といいます (物体の変形は複雑なので高校物理では扱えないし,本質ではありません)。. 剛体が登場するのは,「物体の大きさが無視できない」ような運動を扱う場合です。. これだけ聞くと . PDF ラグランジュの運動方程式 (続き) - Kobe University. 質量m の質点が、原点を中心とする半径1 の円(x2 + y2 = 1)の上を滑る。 この質点が、点(x;y;z) = (1;0;1) とバネでつながれているときの運動を求める。 重力と摩擦は無視する。バネ定数はk、自然長は0 とする。 (a) x 軸となす角度 を一般化座標とする。たとえば . 慣性モーメントと回転の運動方程式 - 大学物理の独言. 質点の運動について考えるのは力学では最も初歩的で基礎となるが、実際のところ質点として考えることのできる物体は多くなく、大抵の場合はその回転運動などの要素も考慮しなければならない。 そこで、剛体という概念を導入し、もう少し日常で起こる現象に近づいた考察を試みるので . ラグランジュ運動方程式の導出 - 物理メモ. 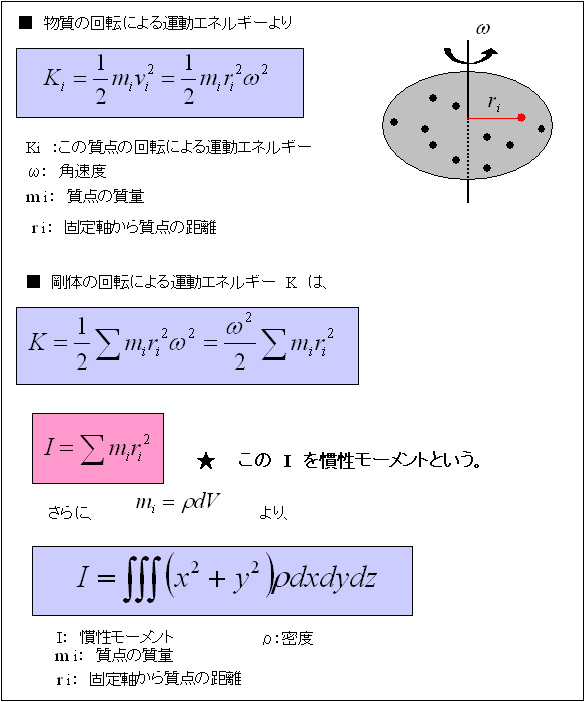
ラグランジアンとラグランジュの運動方程式の導出. 式 (12)に式 (6)を代入する。. d dt( ∂ T ∂ ˙qi) − ∂ T ∂ qi + ∂ V ∂ qi = 0 ・ ・ ・ (13) ポテンシャル V(q1, ⋯, qn) は、速度 ˙qi を含まないから、. ∂ V ∂ ˙qi = 0. この式を式 (13)に挿入する。. d dt( ∂ T ∂ ˙qi フェフ 姉さん 痩せ た





